Problems - Exploring Optics: From Fundamentals to Advanced Applications

Problem 11.1 * Principal planes for a thick lens.

In this problem the transfer matrix for a thick lens is derived. By finding the positions of the principal planes, you will derive that the transfer matrix has the same form as for a thin lens when object, image and focal distances are measured with respect to principle planes.

The transfer matrices which you should use are those for refraction through a spherical interface between two media with refractive indices $n$ , $n'$ to the left and right of the interface, respectively, and with radius of curvature $R$ :

{\cal S} = \left( \begin{array}{cc}1 & -k \\0 & 1 \end{array}\right) \nonumber

(1)

where $k=(n'-n)/R$ , and secondly the matrix ${\cal M}_d$ for propagation through a medium with refractive index $n$ over a distance $d$ .

Consider a thick lens made of a glass of refractive index $n$ with thickness $d$ . For paraxial rays, the thickness can be identified with the distance between the vertices $V_1$ and $V_2$ of the surfaces of the lens.

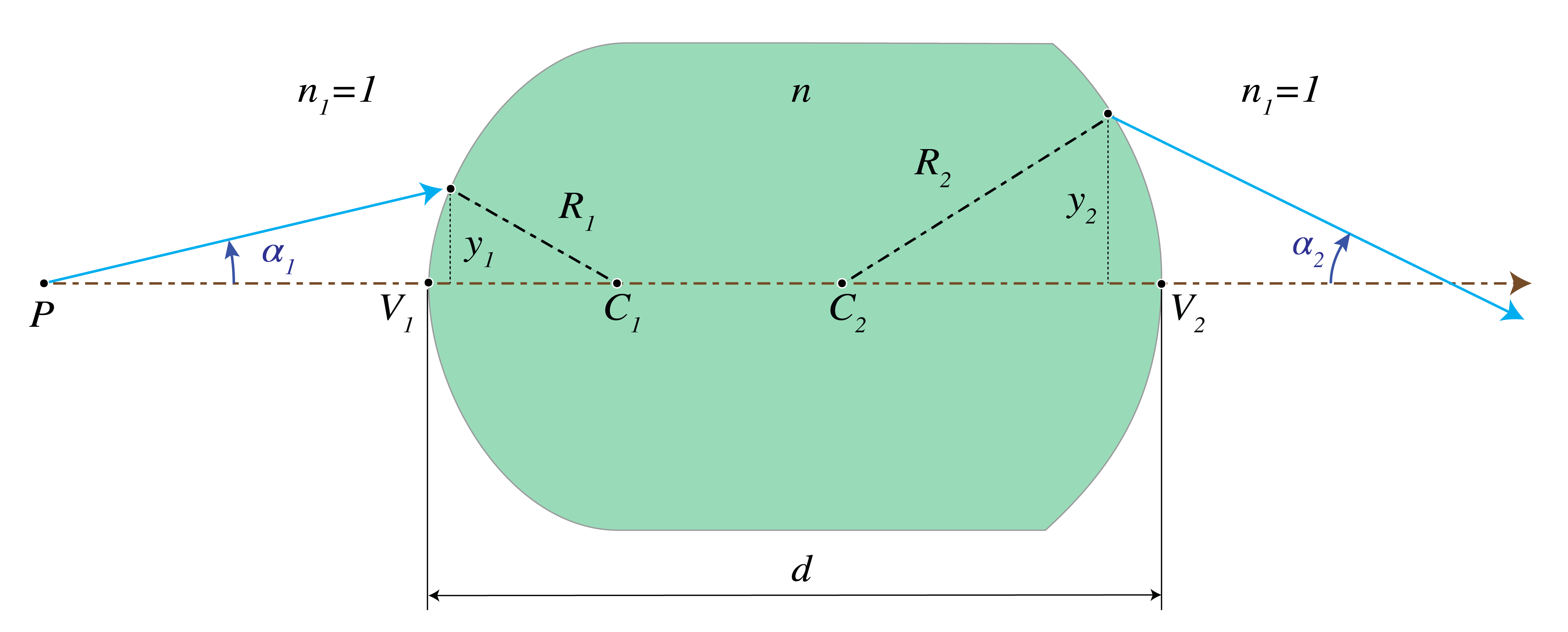
Figure 1:Thick lens geometry showing the two curved surfaces with vertices V₁ and V₂ separated by thickness d. The lens has refractive index n and is surrounded by air, with radii of curvature R₁ and R₂ for the left and right surfaces respectively.

(a) Derive that the transfer matrix between the surfaces through the two vertices of the thick lens is given by:

\begin{align*} {\cal L}_{V_2V_1} = \left( \begin{array}{cc}1 - k_2 \frac{d}{n} & -k_1 -k_2 + k_1 k_2 \frac{d}{n} \\\frac{d}{n} & 1-k_1 \frac{d}{n} \end{array}\right) \end{align*}

(2)

where $k_1= (n-1)/R_1$ and $k_2= (1-n)/R_2$

(b) Show that for $d=0$ the transfer matrix is identical to that for a thin lens given by eq:ray:thin-lens-matrix.

In Section 3.5.7 of the Lecture Notes the primary and secondary principle planes were defined. Let the distance between the primary principle plane ${\cal H}_1$ and vertex $V_1$ be $T_1$ , and let the distance of the second principle plane ${\cal H}_2$ to vertex $V_2$ be $T_2$ as shown in Figure 2). $T_1>0$ and $T_2>0$ if the first principle plane is to the left of $V_1$ and the second principle plane is to the right of $V_2$ , respectively, while $T_1$ and $T_2$ are negative otherwise.

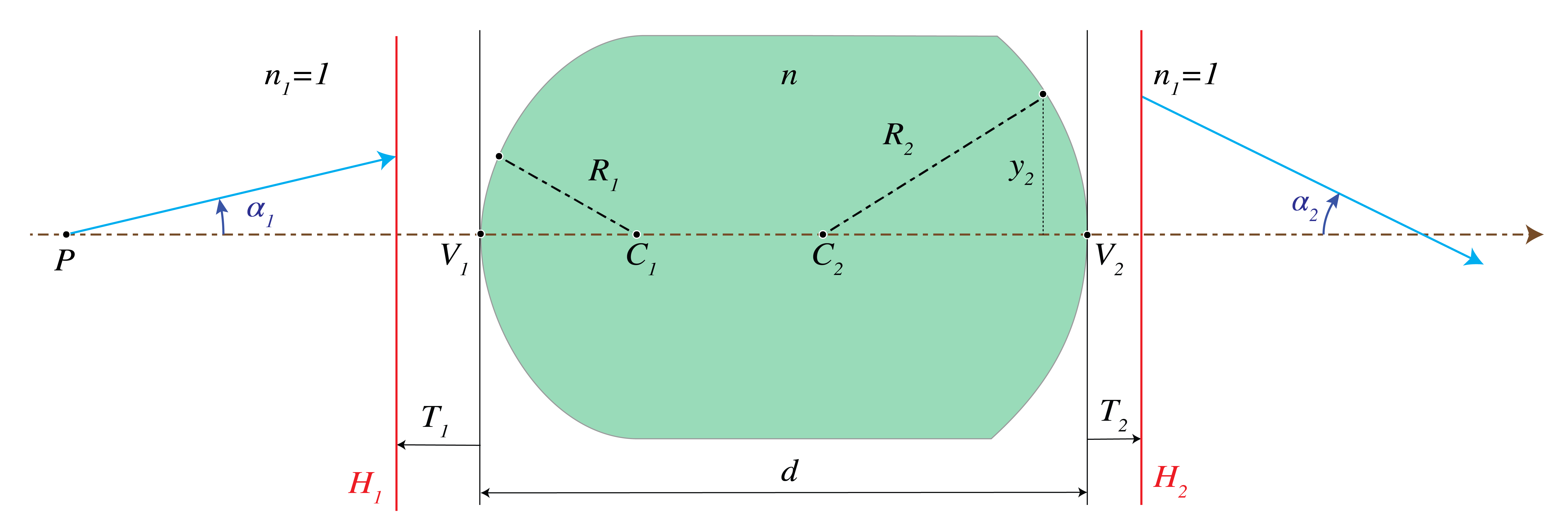
Figure 2:Thick lens with principle planes.

The transformation of a ray from the primary principle plane ${\cal H}_1$ to the secondary principle plane ${\cal H}_2$ is:

\left( \begin{array}{c}\alpha_1 \\y_1 \end{array}\right) = {\cal L}_{{\cal H}_1{\cal H}_2} \left( \begin{array}{c}\alpha_2 \\y_2 \end{array}\right),

(3)

where

\begin{align*} {\cal L}_{{\cal H}_2{\cal H}_1} = {\cal M}_{ T_2} {\cal L}_{V_2 V_1} {\cal M}_{T_1}, \end{align*}

(4)

(c) By using the following abbreviation for the matrix Eq. (2):

\begin{align*} \left( \begin{array}{cc}1 - k_2 \frac{d}{n} & -k_1 -k_2 + k_1 k_2 \frac{d}{n} \\\frac{d}{n} & 1-k_1 \frac{d}{n} \end{array}\right) = \left( \begin{array}{cc}a_{11} & a_{12} \\a_{21} & a_{22} \end{array}\right), \end{align*}

(5)

derive that:

\begin{align*} {\cal L}_{{\cal H}_2{\cal H}_1} = \left( \begin{array}{cc}a_{11} + T_1 a_{12} & \; a_{12} \\T_2 (a_{11} +T_1 a_{12}) + a_{21} + T_1 a_{22} & \; a_{22} + T_2 a_{12} \end{array}\right) \end{align*}

(6)

(d) The principle planes are conjugate (i.e. they are each other images) with unit magnification. Derive from this fact that the locations of the principle planes are given by:

\begin{align*} T_2&=\frac{1-a_{22}}{a_{12} }\\ T_1&= \frac{1-a_{11}}{a_{12}} \end{align*}

(7)

With the solutions for $T_1$ and $T_2$ the system matrix between the principal planes becomes:

{\cal L}_{{\cal H}_2{\cal H}_1} = \left( \begin{array}{cc}1 & a_{12} \\0 & 1 \end{array}\right)

(8)

which has the same shape as the transfer matrix for a thin lens.

(e) Show that the back focal point is at distance $1/a_{12}$ from the secondary principle plane and that the front focal plane is at distance $1/a_{12}$ from the primary principle plane.