Problems - Exploring Optics: From Fundamentals to Advanced Applications

Problem 4.1 Consider a time-harmonic plane wave with real electric field which with respect to a Cartesian coordinate system $(x,y,z)$ is given by:

\begin{align*} \mathbf{E}(z,t)= A \sin\left(k z-\omega t + \pi/2\right) \widehat{\mathbf{x}}+ A \sin\left(k z-\omega t \right) \widehat{\mathbf{y}} \end{align*}

(1)

where $A$ is a positive real number.

(a) Write this electric field as the real part of a complex field.

(b) What is its corresponding Jones vector?

(c) What is the polarization of this electric field? Make a drawing of the electric field vector in the $(x,y)$ -plane at $z=0$ as function of time for an observer that is looking towards the source of the field.

(d) The beam passes normally through a linear polarizer whose transmission axis makes an angle of $45 \degree$ with the positive $x$ -axis. What is the Jones matrix of this linear polarizer?

(e) Derive the real electric field transmitted by the linear polarizer as function of $z$ and $t$ .

(f) What is the state of polarization of the transmitted beam?

(g) What is the intensity of the transmitted beam?

(h) What happens to the difference in energy between the incident and transmitted beam?

Problem 4.2 Partial linear polarization.

Consider a light beam that is partially linear polarized. Show that the degree of polarization is given by

\frac{I_{max}-I_{min}}{I_{max}+I_{min}}.

(2)

where $I_{max}$ and $I_{min}$ are the maximum and minimum of the light transmitted through a linear polarizer when it is turned through 360 degrees.

Problem 4.3 In this problem we consider an optical isolator as shown in Figure 1. In the setup, light can pass in one direction, but it cannot go back. This can for example be used to prevent laser light from going back into the laser source, hereby preventing unwanted effects such as intensity and frequency instabilities.

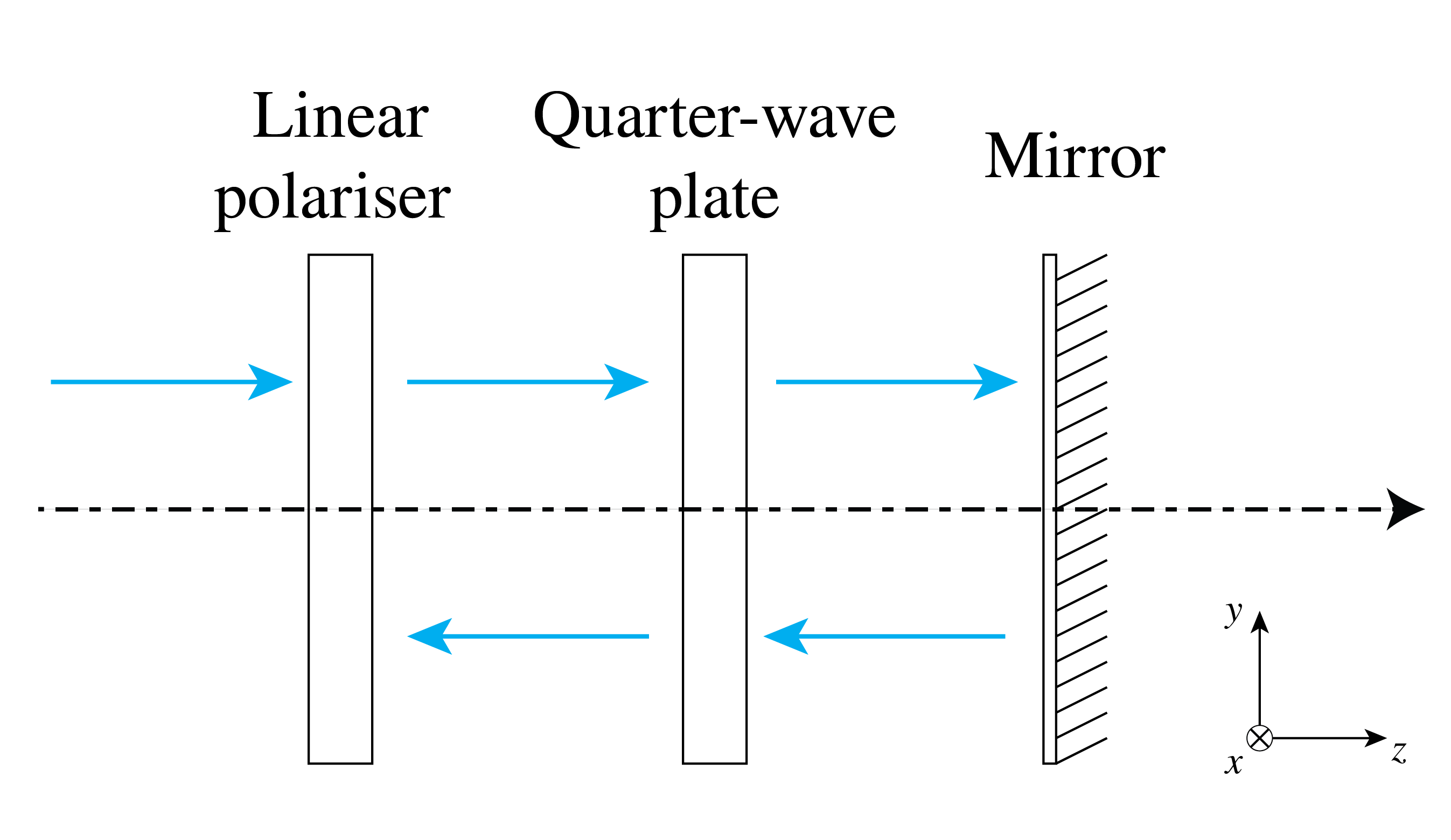
Figure 1:Schematic of a simple optical isolator.

(a) Give the Jones matrix for a linear polarizer $\mathcal{P}$ that polarizes light in the vertical direction (i.e. the $y$ -direction).

(b) Now we rotate the linear polarizer by $\theta=\pi/4$ anti-clockwise. Find the Jones matrix for the rotated polarizer $\mathcal{P}_{\pi/4}$ . Check your result by verifying that:

\mathcal{P}_{\pi/4}\begin{pmatrix}1\\ 1\end{pmatrix}=\begin{pmatrix}1\\ 1\end{pmatrix}, \quad \mathcal{P}_{\pi/4}\begin{pmatrix}1\\ -1\end{pmatrix}=\begin{pmatrix}0\\ 0\end{pmatrix}.

(3)

(c) Give the Jones matrix $\mathcal{Q}$ for the quarter-wave plate of which the slow axis points in the vertical direction (i.e. the $y$ -direction).

(d) Suppose we send light through the linear polarizer and the quarter-wave plate. Then the light is partially transmitted and partially reflected by the mirror. The reflected light passes again through the quarter-wave plate and the polarizer. Using Jones matrices calculate the state of the light that exits.

A video demonstration of this optical isolator can be viewed at ^[1] (or search for “MIT optical isolator” on Youtube).

Problem 4.4 Phase plates.

We consider a time-harmonic plane wave which propagates in the positive $z-$ direction.

(a) Suppose we have a linear polarizer orientated such that the angle with the positive $\hat{\mathbf{x}}$ -axis is $+45^o$ . Behind the linear polarizer there is a half wave plate with fast axis orientated parallel to the $\hat{\mathbf{y}}$ -axis. What is the orientation of the polarization of the wave transmitted first by the linear polarizer and then by the half wave plate when the incident wave is linear polarized parallel to the $\hat{\mathbf{x}}$ -axis?

(b) What is the intensity of the transmitted wave when the incident wave in a) has amplitude $A$ ?

(c) Suppose now that the half wave plate behind the linear polarizer with angle $45^o$ with the $x$ -axis, is replaced by a quarter wave plate with the fast axis parallel to the $y$ -axis. What is the polarization of the transmitted light when the incident wave is linearly polarized parallel to the $\hat{\mathbf{x}}$ -axis?

(d) What is the intensity of the transmitted wave when the incident wave in c) has amplitude $A$ ?

(e) Suppose that an incident linear polarized wave which is polarized parallel to the $x$ -axis light is first transmitted by a quarter wave plate of which the fast axis makes an angle of $+45^o$ with the positive $x$ -axis, and is then transmitted by a half wave plate with fast axis parallel to the $y$ -axis.

What is the polarization of the transmitted light if the incident wave is polarized parallel to the $\hat{\mathbf{x}}$ -axis?

Problem 4.5 Jones Matrices.

Verify for each of the following matrices whether they correspond to a linear polarizer, a wave plate or are neither. Also specify the direction of the linear polarizer and the type of the wave plate.

(a)