Problems - Exploring Optics: From Fundamentals to Advanced Applications

Problem 6.1 Michelson interferometer.

(a) A Michelson interferometer is illuminated with monochromatic light. One of its mirrors is moved 2.53 $\times10^{-5}$ m, and it is observed that 92 fringe-pairs, bright and dark, pass by the screen during the process. Determine the wavelength of the incident beam.

(b) Suppose that for the wavelength determined under a), only 23 fringes can be distinguished when one of the mirrors in moved over 2.53 $\times10^{-5}$ m. What is the coherence length and coherence time of the source?

Problem 6.2 Two sources.

(a) Suppose the two sources $S_1$ and $S_2$ are coherent and emit radio waves with a wavelength of 3 m. The two sources are in phase, and they are separated by 3 m. How far should an observer be directly in front of either source (along a perpendicular to $\overline{S_1S_2}$ , see Figure 1), to encounter a minimum of irradiance?

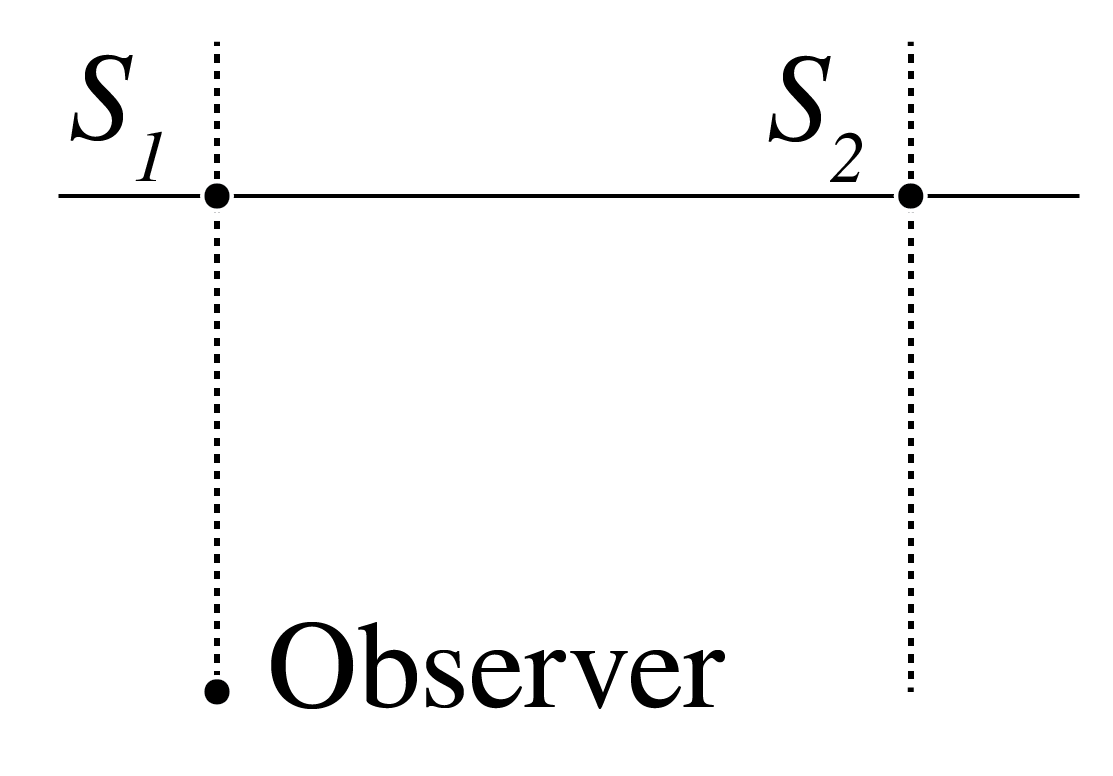
Figure 1:Geometry for two-source interference problem. Two coherent radio wave sources S₁ and S₂ are separated by 3 m, and an observer is positioned at a perpendicular distance from the baseline connecting the sources. The path difference between waves from the two sources determines whether constructive or destructive interference occurs at the observation point.

(b) Suppose that the sources are mutually incoherent. There distance is again 3 m and the center wavelength is 3 m. What should be the perpendicular distance to the two sources of two points that have distance of 6 m when the degree of mutual coherence is 0.866. You may use the formula for quasi-monochromatic light.

Problem 6.3 Reflection coating.

A thin planar film with an index of refraction of $n_2=1.5$ is immersed in air with $n_1=1$ as shown in Figure 2. A plane wave with a wavelength of $\lambda=632$ nm hits the film at an angle of incidence of $\theta_1=30$ ° with respect to the normal on the surface. Some of the light will reflect directly at the air-film interface, and some of the light will make one or several round trips through the film and then adds to the directly reflected light. In this exercise we only consider the directly reflected light at the air-film interface and the light that makes one round trip inside the film.

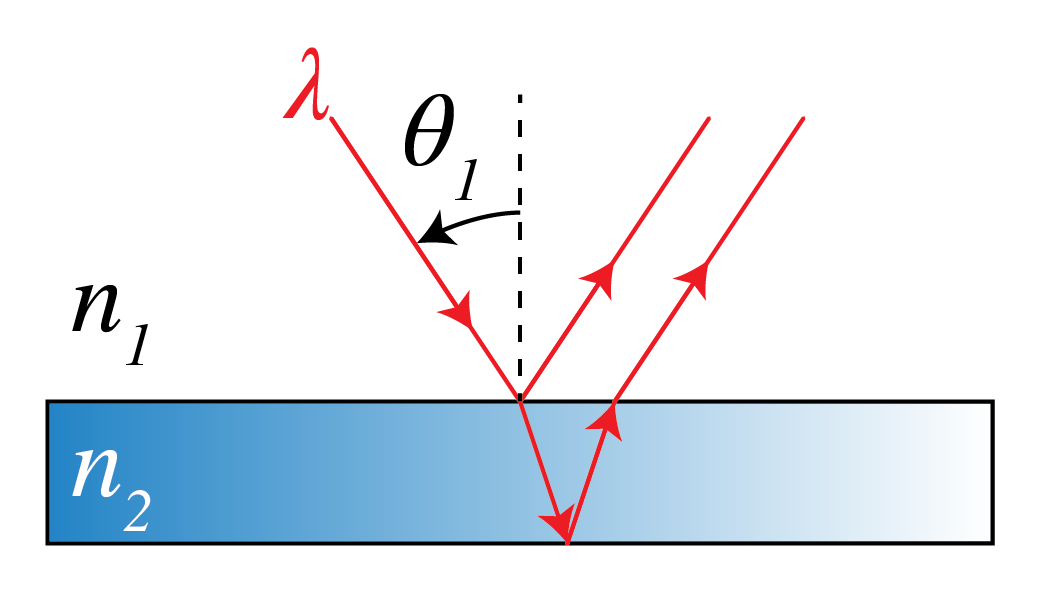
Figure 2:Thin film illuminated by a plane wave.

(a) What is the smallest film thickness for which we get a maximum reflectance of the film? We recall that the light that is reflected directly at the air-glass interface gets a phase shift of $\pi$ .

(b) Describe what happens to the reflected field when the film is 237 nm thick?

Problem 6.4 Let a point source $P$ be at $\mathbf{r}_p =(0,0,d)$ where $d>0$ is the distance to a mirror in the $z=0$ plane (Figure 3).

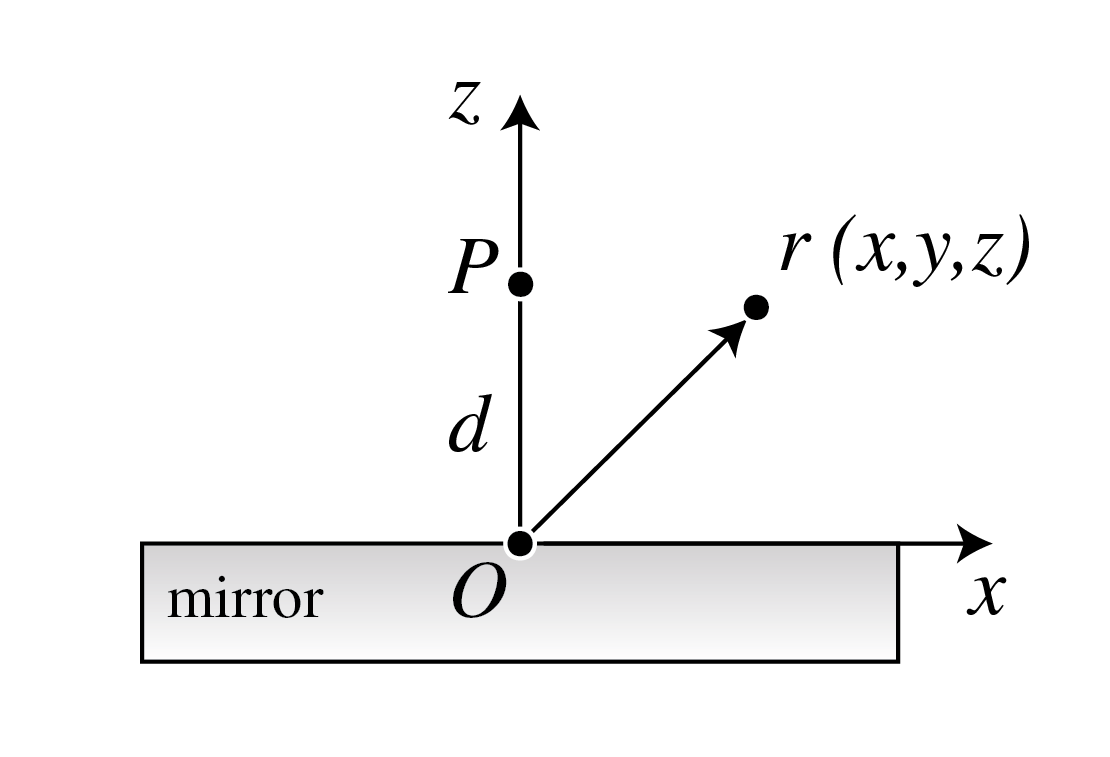
A point source P above a perfect mirror. — Figure 3:A point source $P$ above a perfect mirror.

The point source emits a time-harmonic field with complex amplitude in a point $\mathbf{r}=(x,y,z)$ given by

\begin{align*} U_{p}(\mathbf{r}) = \frac{e^{i k \sqrt{x^2 + y^2 + (z-d)^2}}}{\sqrt{ x^2 + y^2 + (z-d)^2}}. \end{align*}

(1)

Assume that the mirror is perfect, i.e. the total field on the mirror surface vanishes: $U_{total}(x,y,0)=0$ .

(a) Derive the formula for the reflected and the total field in an arbitrary point $\mathbf{r}=(x,y,z)$ with $z>0$ .

(b) What is the total intensity in an arbitrary point $\mathbf{r}$ ?

(c) Compute the intensity on the $z$ -axis for $0\leq z \leq d$ . What is the period of the fringes? For which $z$ -value does the intensity vanish?

(d) Derive the intensity for $x=y=0$ and $z>d$ . Show that for very large $z$ the intensity is zero when $d=(2m+1)\lambda/4$ for $m=0,1,2,\ldots$ .

(e) Suppose that the coherence time of the field radiated by the point source is $\tau_c$ . For which distances $d$ does there occur no interference anywhere in $z>2d$ between the field directly radiated by the point source and the reflected field? What is the intensity in this case?

Problem 6.5 Two sources and two pinholes.

Two independently radiating small sources $S_1$ and $S_2$ emits light with center frequency $\omega_c$ and bandwidth $\Delta \omega \ll \omega_c$ . (see the figure below). The coherence time of the sources is thus $\tau_c=\Delta \omega$ . At a distance $z_1$ a first screen with pinholes $P_1$ and $P_2$ is placed. Far away, at (Fraunhofer) distance $z_2$ from the first screen a second screen is placed. Which of the following statements are true

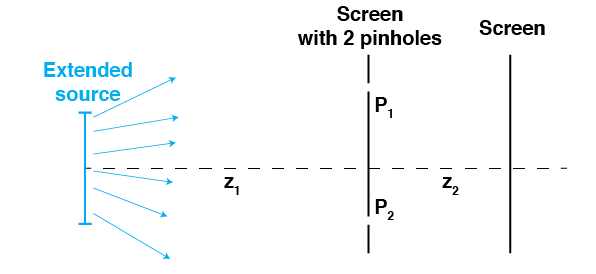
Two independent small sources S_1 and S_2 with 2 pinhole and a screen (Exercise 4). — Figure 4:Two independent small sources $S_1$ and $S_2$ with 2 pinhole and a screen (Exercise 4).

(a) The interference fringes disappear if the difference between distances: $|P_1S_1-P_2S_1|$ and $|P_1S_2-P_2SA_2|$ are larger than $l_c=\tau_c c$ .

(b) There are no fringes on the second screen if one of the sources $S_1$ or $S_2$ is switched off.

(c) There can only be fringes on the second screen when there is only one source.

(d) The interference fringe contrast on the second screen decreases when $z_2$ is decreased.

(e) The interference fringe contrast on the second screen decreases when $z_1$ is increased.

(f) There are no fringes when the pinholes are of the order of a wavelength and one of the pinholes is closed.

(g) There are interference fringes on the screen when the distance $z_1$ is large enough and the pinholes have width of many wavelength and one of them is closed.

(h) If more pinholes are added between $P_1$ and $P_2$ the interference fringes become broader.

Problem 6.6 Fabry-Perot interferometer.

[Problem under construction]